Advanced Simulation: Biology

Here we described advanced usage of the simulation functionality, in particular how to go beyond the built-in biology options for RaftParameters. Covered in this section are AbstractLand and AbstractGrowthDeathModel, i.e. for the purposes of this discussion we would refer to death by beaching as a biological effect.

For advanced Julia users

The biological functionality is implemented using Callbacks from OrdinaryDiffEq.jl.

Overview

Biological effects are implemented on top of physics effects in a modular fashion. After each step of the integration, a condition function is called on the current state. If this condition returns true, an affect! function is called that applies the desired logic. Hence, what is required of the user is to implement the appropriate structure and a condition function that checks whether to do something and an affect! function that does that thing. In Sargassum.jl, these functions are directly defined on the structure, e.g.

struct MyBiology <: AbstractGrowthDeathModel
    # fields
end

(b::MyBiology)(u, t, integrator)    # condition
(b::MyBiology)(integrator)          # affect!

Here, u is the solution vector as described in RaftParameters, t is the current time and integrator comes from the underlying differential equations solver. In brief, integrator contains all the information required to carry out the integration. The most relevant fields are:

• integrator.u and integrator.t for the solution and time at the current step.

• integrator.uprev and integrator.tprev for solution and time at the previous step.

• integrator.sol for the full state of the solution; this can be called like a function at an arbitrary time to interpolate the solution at that value, or previous solutions and times can be accessed via integrator.sol.u and integrator.sol.t.

• integrator.p for the current RaftParameters.

In Sargassum.jl, the tools for handling the actual growth or death of clumps are already built-in via the grow! and kill! functions.

The grow! and kill! Functions

The grow! and kill! functions handle the mechanics of creating a new clump at location or killing a clump with index i or a set of clumps with indices [i1, i2, ...]. The signatures are

grow!(integrator; location)
kill!(integrator, index_or_indices)

kill! is straightfoward, it kills the clump(s) with index_or_indices. The implication is that it is up to the user to determine the indices of clumps that are to be killed. One pattern for accomplishing this is to let MyBiology have fields of the Vector type named growths and deaths which are populated during the call to condition. Then, the affect! function simply calls kill!(integrator, deaths) to execute the logic.

The grow! function has an optional argument location, which can be a pre-defined flag, an integer, or a [x, y] vector. The default value is the flag "parent".

The possible flags are:

• "parent": A parent clump is chosen randomly among clumps that already exist, and the new clump is placed MarkdownAST.LineBreak()

a distance integrator.rp.springs.L away and at a uniformly random angle from it.

• "com": The same as "parent", except the center location is at the center of mass of the raft.

If location is an Integer with value i, then the new clump will be grown with ith clump (by vector location) as its parent.

If location is a Vector{<:Real}, the new clump will be placed at those [x, y] coordinates.

Custom AbstractLand

We begin by describing how to build a custom AbstractLand object since the affect! logic is usually simpler than a AbstractGrowthDeathModel. We will recreate the built in Land to see how it is done. Referring to our earlier example, what is required of us is of the form

struct MyLand <: AbstractLand
    # fields
end

(b::MyLand)(u, t, integrator)    # condition
(b::MyLand)(integrator)          # affect!

Before proceeding, we should make sure we decide on the logic. In this case, the condition should check each clump to see if it is on land. If any clumps are on land, it should return true to signal that the affect! should act. Inside affect! we should call kill!(integrator, inds) on those inds that identify beached clumps. To avoid calculating the land status of clumps twice, we could add a field to MyLand called deaths and populate it with clumps that have reached land.

struct MyLand <: AbstractLand
    deaths::Vector{Int64}

    # constructor that populates `death` with an empty vector
    function MyLand()
        return new(Int64[])
    end
end

Examining LAND_ITP and referring to interpolants, we see that a clump with position (x, y) is on land if field(LAND_ITP, :land)(x, y) == 1. Therefore,

### condition
function (l::MyLand)(u, t, integrator)
    empty!(l.deaths)                        # reset deaths
    N = size(u, 2)                          # number of clumps
    living = (1:N)[integrator.p.living]     # indices of clumps that are actually alive (see `RaftParameters`)
    for i in living
        if field(LAND_ITP, :land)(u[:,i]...) == 1
            push!(l.deaths, i)
        end
    end

    if length(l.deaths) > 0
        return true # there is at least one death to resolve
    else
        return false
    end
end

### affect!
function (l::MyLand)(integrator)
    # we already know the clumps to kill, so we only have to invoke `kill!`
    kill!(integrator, l.deaths)

    @info "Killed clumps $(l.deaths) after $(integrator.t - integrator.p.ics.tspan[1]) days." # just for testing
    return nothing
end

Let's try this out by simulating some clumps close to land.

tspan = (DateTime(2018, 4, 13), DateTime(2018, 5, 3)) .|> datetime2time
ics = InitialConditions(tspan, range(-86.0, -81.0, length = 5), range(16.0, 18.0, length = 5), to_xy = true)
n_clumps_max = size(ics.ics, 2)
clumps = ClumpParameters()
springs = BOMBSpring(1.0, ΔL(ics))
connections = ConnectionsNearest(n_clumps_max, 2)
gd_model = ImmortalModel()
land = MyLand() # this is us!

rp = RaftParameters(
    ics = ics,
    clumps = clumps,
    springs = springs,
    connections = connections,
    gd_model = gd_model,
    land = land,
    n_clumps_max = n_clumps_max
)

rtr = simulate(rp)

fig = Figure()
ax = Axis(fig[1, 1], limits = (-100, -80, 15, 25))
viz!(ax, rtr)
viz!(ax, rtr.trajectories[2], color = :red)
viz!(ax, rtr.trajectories[16], color = :red)
viz!(ax, rtr.trajectories[12], color = :red)
land!(ax)

fig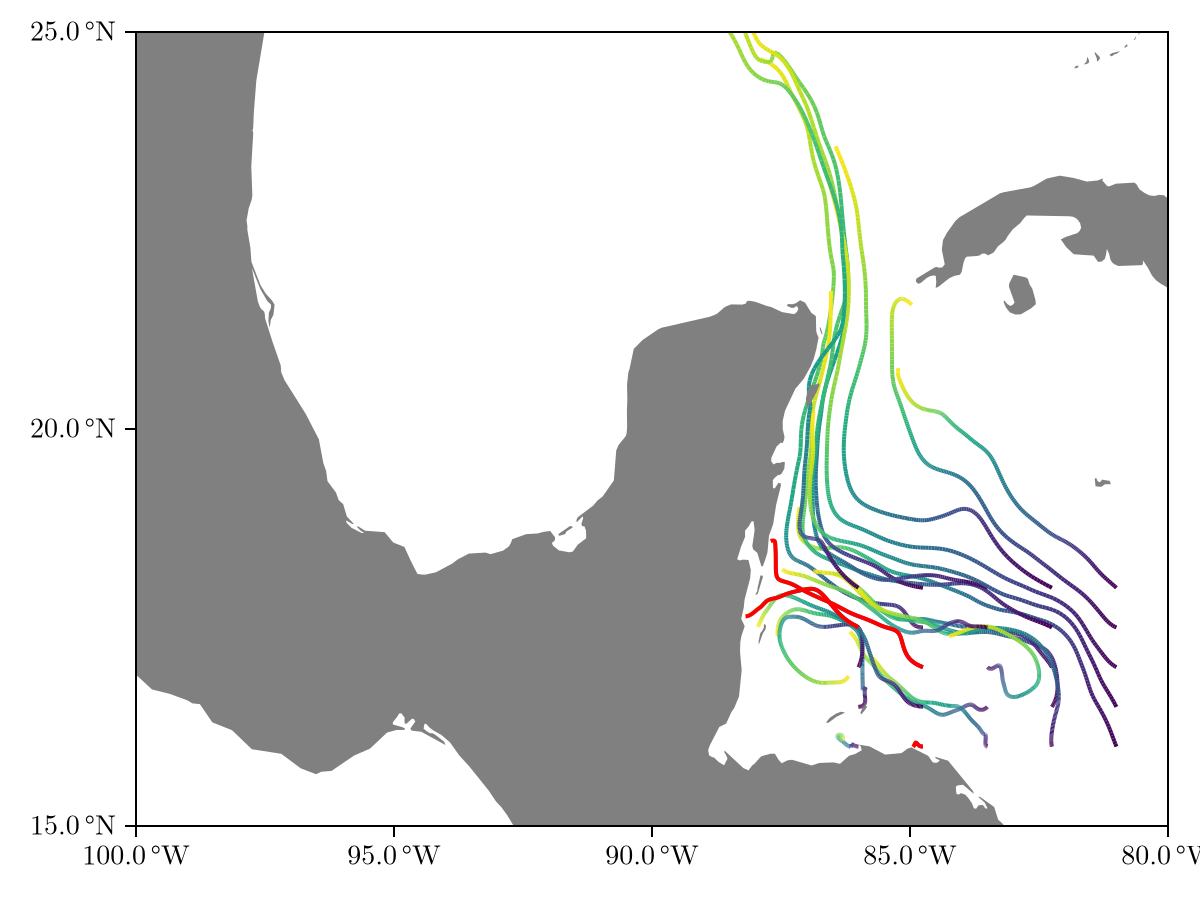

We see that three clumps (highlighted in red) get too close to land and are removed from the integration. Programmatically, we note that e.g. clump 2 died after circling around its initial location with small velocity for a few days.

rtr.trajectories[2]

Trajectory[(6677.0, 6681.9), 50 pts]

We could, for example, define CloseEnoughLand <: AbstractLand that kills clumps whose positions have been within a certain distance of land for a prescribed time.

Custom AbstractGrowthDeathModel

The process of building a custom biological model is identical to that of building an AbstractLand. As we saw previously, the general scaffolding is

struct MyBiology <: AbstractGrowthDeathModel
    # fields
end

(b::MyBiology)(u, t, integrator)    # condition
(b::MyBiology)(integrator)          # affect!

In principle, there's nothing preventing an AbstractGrowthDeathModel from using LAND_ITP to compute its effects, i.e. one could pass land = NoLand() to RaftParameters and have their AbstractGrowthDeathModel contain land effects in addition to other biology.

We will define a simple biological model to illustrate some possibilities, but appropriate application of kill! and grow! allows essentially arbitrary behavior. The logic for our example will be

• after 5 days, kill half (rounded down) of the most southerly clumps (do this once)

• after 10 days, grow a clump next to each living clump in the "parent" sense of grow! (do this once)

Of course, this model is not very realistic, but it will illustrate the main ideas. First, we define our MyBiology object. It is useful (although not required) to have growths and deaths fields to avoid a doubling of computational effort. We also need Bool flags to ensure that the proposed events only happen once. This also requires a mutable struct to update these flags.

mutable struct MyBiology <: AbstractGrowthDeathModel
    growths::Vector{Int64}
    deaths::Vector{Int64}
    five_days_event::Bool
    ten_days_event::Bool

    # constructor
    function MyBiology()
        return new(Int64[], Int64[], false, false)
    end
end

Next, we implement the logic.

### condition
function (bio::MyBiology)(u, t, integrator)
    empty!(bio.deaths)                      # reset deaths
    empty!(bio.growths)                     # reset deaths
    N = size(u, 2)                          # number of clumps
    living = (1:N)[integrator.p.living]     # indices of clumps that are actually alive (see `RaftParameters`)
    t0 = integrator.p.ics.tspan[1]          # initial time

    if t - t0 > 5 && !bio.five_days_event
        ys = u[2,:]
        sp = intersect(sortperm(ys), living) # only kill clumps that are already alive
        to_kill = sp[1:floor(Int64, length(sp)/2)]
        append!(bio.deaths, to_kill)
        bio.five_days_event = true
    end

    if t - t0 > 10 && !bio.ten_days_event
        append!(bio.growths, living) # each clump is a parent
        bio.ten_days_event = true
    end

    if length(bio.deaths) > 0 || length(bio.growths) > 0
        return true # there is at least one growth or death to resolve
    else
        return false
    end
end

### affect!
function (bio::MyBiology)(integrator)
    for i in bio.growths
        grow!(integrator, location = i)
    end

    kill!(integrator, bio.deaths) # does nothing if `bio.deaths` is empty

    @info "Killed clumps $(bio.deaths) and grew clumps $(bio.growths) after $(integrator.t - integrator.p.ics.tspan[1]) days." # just for testing
    return nothing
end

Let's try this out with a simulation. It's important to remember that n_clumps_max needs to be set large enough to accommodate the possible growth. Since the number of clumps can at most double, we'll take n_clumps_max to be double the initial number of clumps.

tspan = (DateTime(2018, 4, 13), DateTime(2018, 5, 3)) .|> datetime2time
ics = InitialConditions(tspan, range(-55.0, -50.0, length = 8), range(5.0, 10.0, length = 8), to_xy = true)
n_clumps_max = 2*size(ics.ics, 2) # note the 2
clumps = ClumpParameters()
springs = BOMBSpring(3.0, ΔL(ics))
connections = ConnectionsNearest(n_clumps_max, 2)
gd_model = MyBiology() # this is us!
land = Land()

rp = RaftParameters(
    ics = ics,
    clumps = clumps,
    springs = springs,
    connections = connections,
    gd_model = gd_model,
    land = land,
    n_clumps_max = n_clumps_max
)

rtr = simulate(rp)
viz(rtr, limits = (-65, -45, 5, 15))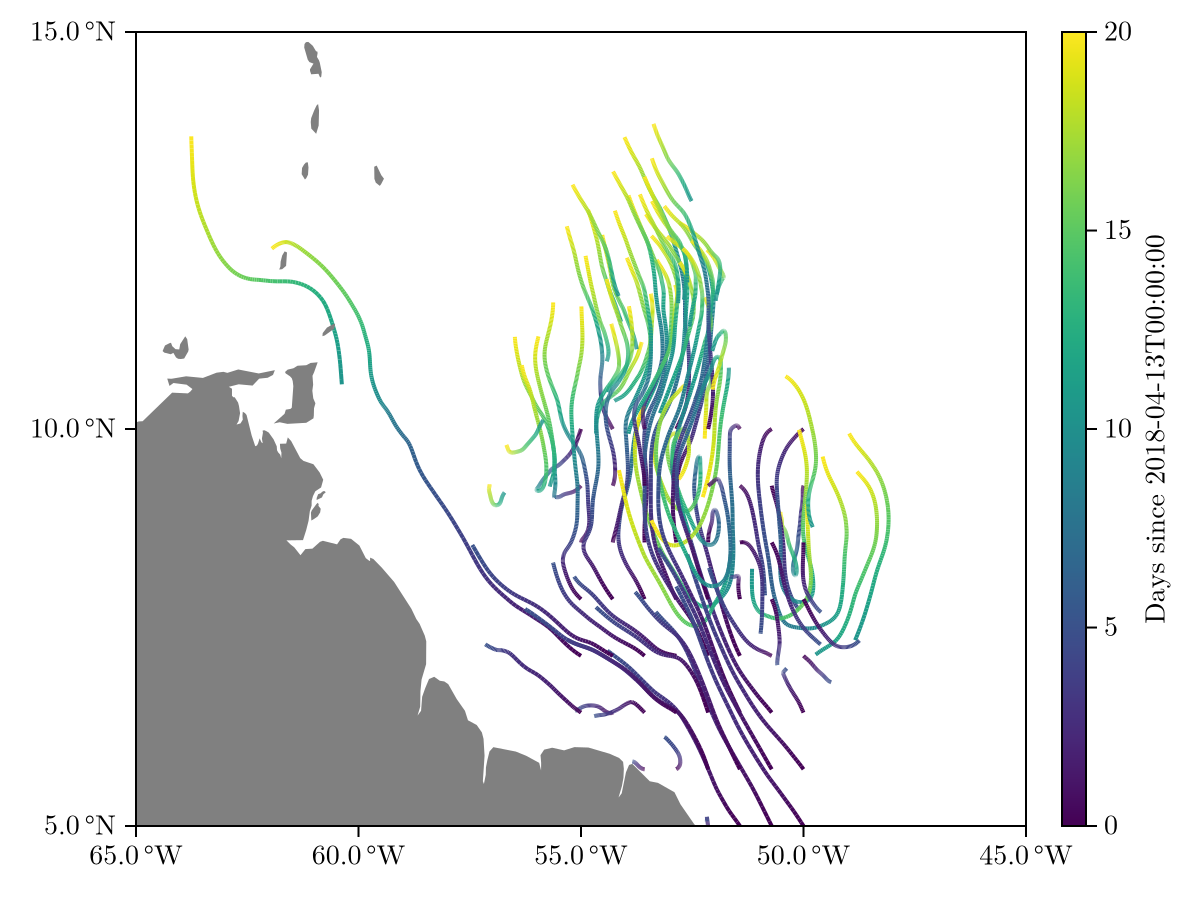

We can further visualize the number of clumps as a function of time to see more clearly that our biological model had the intended effect.

with_theme(theme_latexfonts()) do # with_theme since don't want degrees N/S etc.
    fig = Figure()
    ax = Axis(fig[1, 1], xlabel = "Days since April 13, 2018", ylabel = "Number of living clumps")
    ts = rtr.com.t |> x -> x .- first(x)
    lines!(ax, ts, rtr.n_clumps, linewidth = 4, color = :black)
    fig
end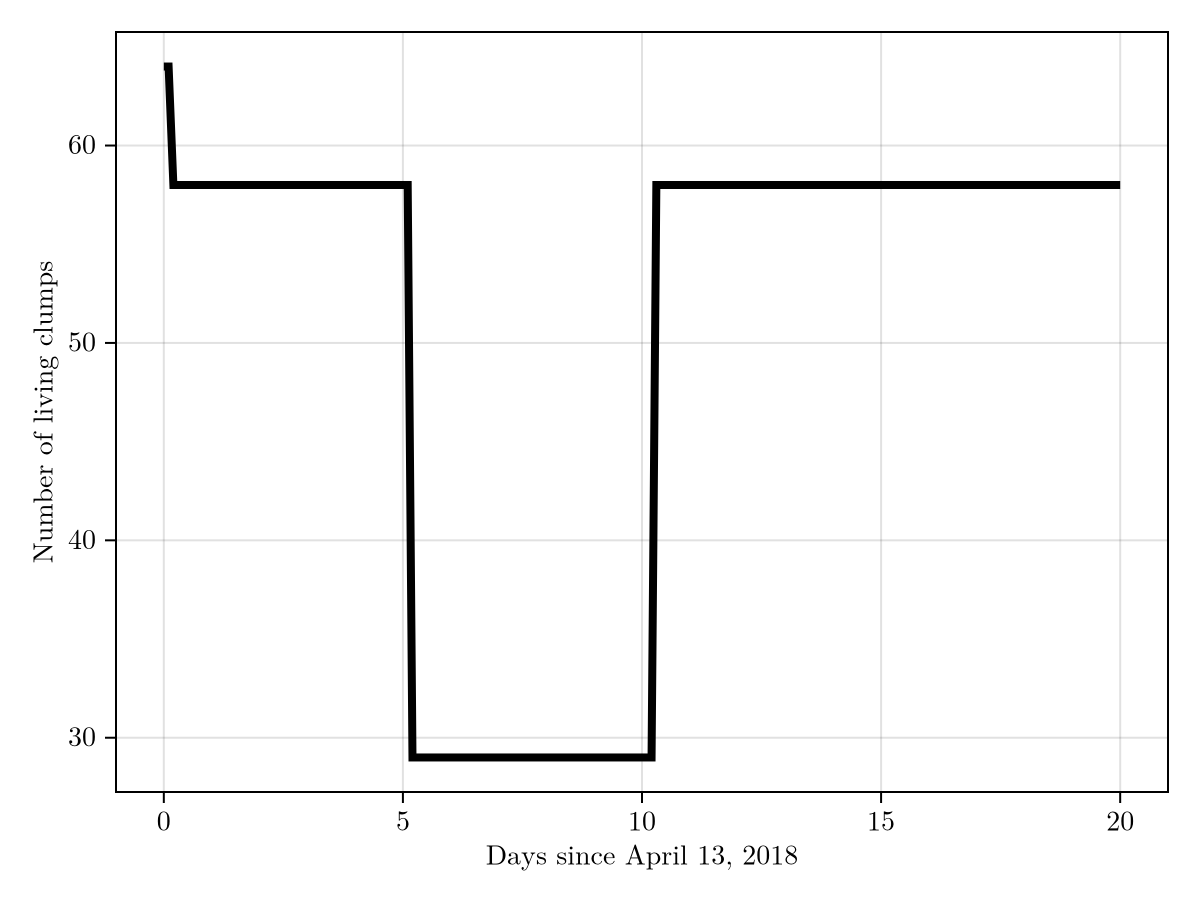

Note that the effects did not take place exactly at 5 and 10 days since they can only be triggered at the end of a step, i.e. in this case they are triggered at the first step such that the integration time is greater than 5 (and 10).