Advanced Simulation: Physics

Here we described advanced usage of the simulation functionality, in particular how to go beyond the built-in physics options for RaftParameters. Covered in this section are InitialConditions, ClumpParameters, AbstractConnections and AbstractSprings.

Initial Conditions

In general, InitialConditions should require the least amount of customization, since an arbitrary set of initial conditions can be passed using the InitialConditions(tspan, xy0; to_xy) constructor. We briefly mention here the interactivity between simulation tools and AFAI tools. In particular, clumps can be initialized according to a SargassumDistribution using the InitialConditions(dist, week, n_weeks, levels; seed) constructor. For example,

dist = SARGASSUM_DISTRIBUTION_PRECOMPUTED[(2018, 4)]
InitialConditions(dist, 1, 2, 3)

This sets up InitialConditions for the first week of April, 2018. The integration will span two weeks and initialize the clumps with level specification 3. The level argument corresponds to the number of clumps initialized; roughly speaking, the higher the level, the more accurately the SargassumDistribution is reproduced. Refer to the full documentation of InitialConditions for more details.

Clumps

A ClumpParameters object has a large number of physics kwargs. For example, we can change the buoyancy δ

ClumpParameters(δ = 1.1)

ClumpParameters[α = 0.002573, τ = 0.02828, R = 0.8678, Ω = 6.283, σ = 0.0]

The quantities α (~ wind strength) and τ (~ strength of inertial effects) depend on a (~ clump size) and δ. Occasionally it is useful to "force" specific values. This can be accomplished using the direct constructor ClumpParameters(α, τ, R, Ω, σ), for example

clp = ClumpParameters()
my_α = 0.1
my_τ = 0.2
my_clp = ClumpParameters(my_α, my_τ, clp.R, clp.Ω, clp.σ)

ClumpParameters[α = 0.1, τ = 0.2, R = 0.7883, Ω = 6.283, σ = 0.0]

This sets α and τ while leaving the other parameters set to their defaults.

Springs

There are two main objects to consider, AbstractConnections which implements the logic determining how connections are formed at each step of the integration, and AbstractSpring which implements the spring physics such as its stiffness function and natural length. First, we describe how to implement a custom AbstractConnections.

How to make ConnectionsFull

We'll create our own version of ConnectionsFull to see how it is done. As a reminder, ConnectionsFull simply connects every clump to every other clump. The first step is to define our actual object, let's say MyConnectionsFull, as a subtype <: of AbstractConnections. Every subtype of AbstractConnections should have a field connections which is similar to a vector of vectors such that that connections[i] is a list of clump indices that are connected to clump i. For example, if MyConnectionsFull[1] = [2, 3], this advises that clump 1 is connected to clumps 2 and 3. It should be initialized such that connections is of length n_clumps_max, i.e. the maximum number of clumps in the simulation.

Clump indexing

As described in RaftParameters, the solution vector u is a 2 x N matrix such that u[:,i] gives the (x, y) coordinates of the ith clump. The indexing in an AbstractConnections is identical.

Our MyConnectionsFull may have any other fields we need, e.g. the ConnectionsNearest has a field neighbors to keep track of how many nearest-neighbors each clump should be connected to. For now, let's just implement the minimum.

struct MyConnectionsFull <: AbstractConnections
    connections::Vector{Vector{Int64}}

    function MyConnectionsFull(n_clumps_max::Integer)
        return new([Int64[] for _ = 1:n_clumps_max])
    end
end

Next, we have to implement the connection logic. This is done by overloading Sargassum.form_connections(con::MyConnectionsFull, u), where u is the solution vector. This function should return the updated connections, i.e.

function Sargassum.form_connections(con::MyConnectionsFull, u)
    # calculate new_connections based on `u` and any extra fields we might have in `con`
    return new_connections
end

In this example, the logic is straightforward: assume that u is 2 x N, then clump 1 should be connected to [2, 3, .. N], clump 2 should be connected to [1, 3, ..., N]. A convenience is provided here, where we can safely indicate that a clump should be connected to itself without error (such a connection is ignored). Therefore, each clump should be connected to [1, 2, ..., N].

function Sargassum.form_connections(con::MyConnectionsFull, u)
    N = size(u, 2)
    new_connections = [collect(1:N) for _ = 1:N]
    return new_connections
end

That's all there is to it. Let's try it out and compare to the stock ConnectionsFull.

tspan = (DateTime(2018, 4, 13), DateTime(2018, 4, 20)) .|> datetime2time
ics = InitialConditions(tspan, range(-55.0, -50.0, length = 5), range(5.0, 10.0, length = 5), to_xy = true)
n_clumps_max = size(ics.ics, 2)
clumps = ClumpParameters()
springs = BOMBSpring(1.0, ΔL(ics))
my_connections = MyConnectionsFull(n_clumps_max) # this is us!
connections = ConnectionsFull(n_clumps_max) # the stock version
gd_model = ImmortalModel()
land = Land()

my_rp = RaftParameters(
    ics = ics,
    clumps = clumps,
    springs = springs,
    connections = my_connections,
    gd_model = gd_model,
    land = land,
    n_clumps_max = n_clumps_max
)

stock_rp = RaftParameters(
    ics = ics,
    clumps = clumps,
    springs = springs,
    connections = connections,
    gd_model = gd_model,
    land = land,
    n_clumps_max = n_clumps_max
)

my_rtr = simulate(my_rp)
stock_rtr = simulate(stock_rp)

fig = Figure()
ax = Axis(fig[1, 1], title = "MyConnectionsFull", limits = (-60, -45, 5, 12))
viz!(ax, my_rtr)
land!(ax)

ax = Axis(fig[1, 2], title = "ConnectionsFull", limits = (-60, -45, 5, 12))
viz!(ax, stock_rtr)
land!(ax)

fig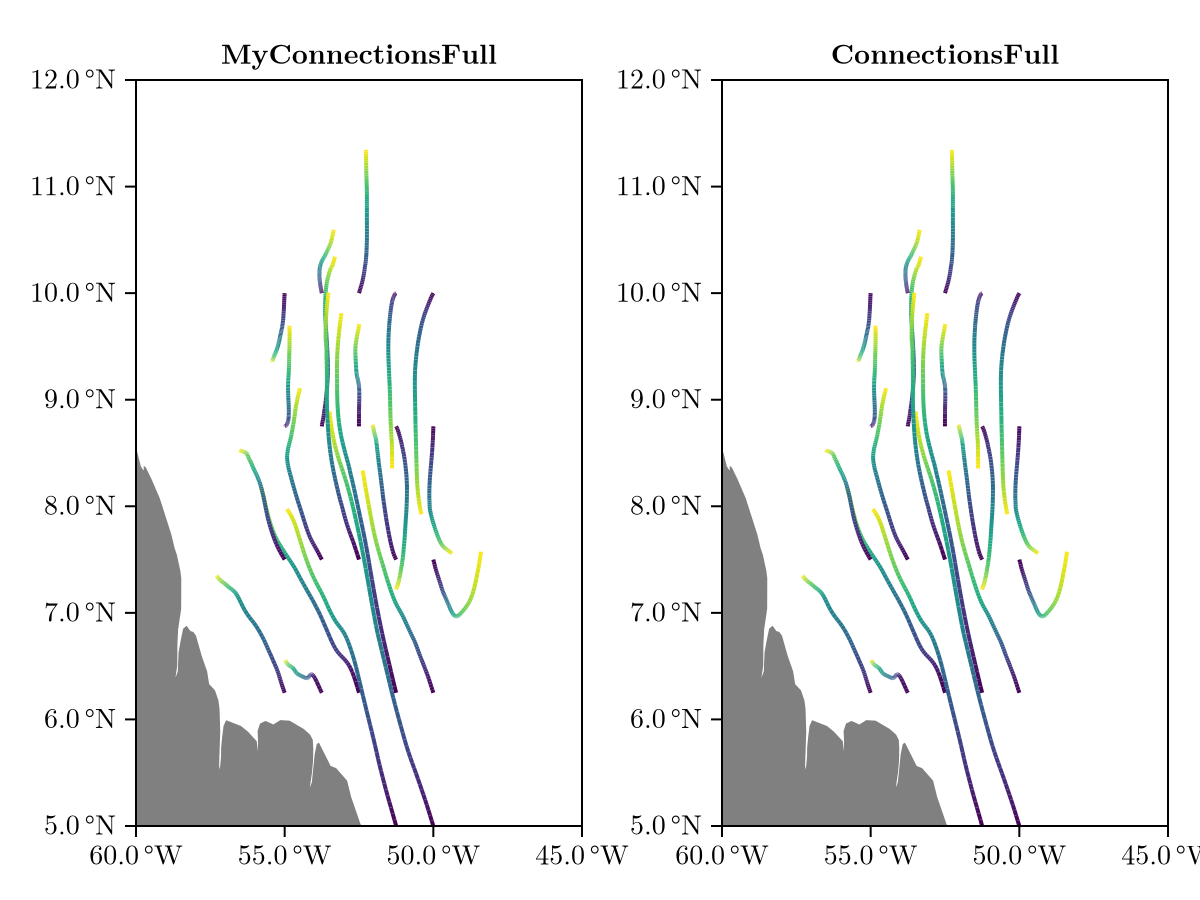

As expected, these look identical.

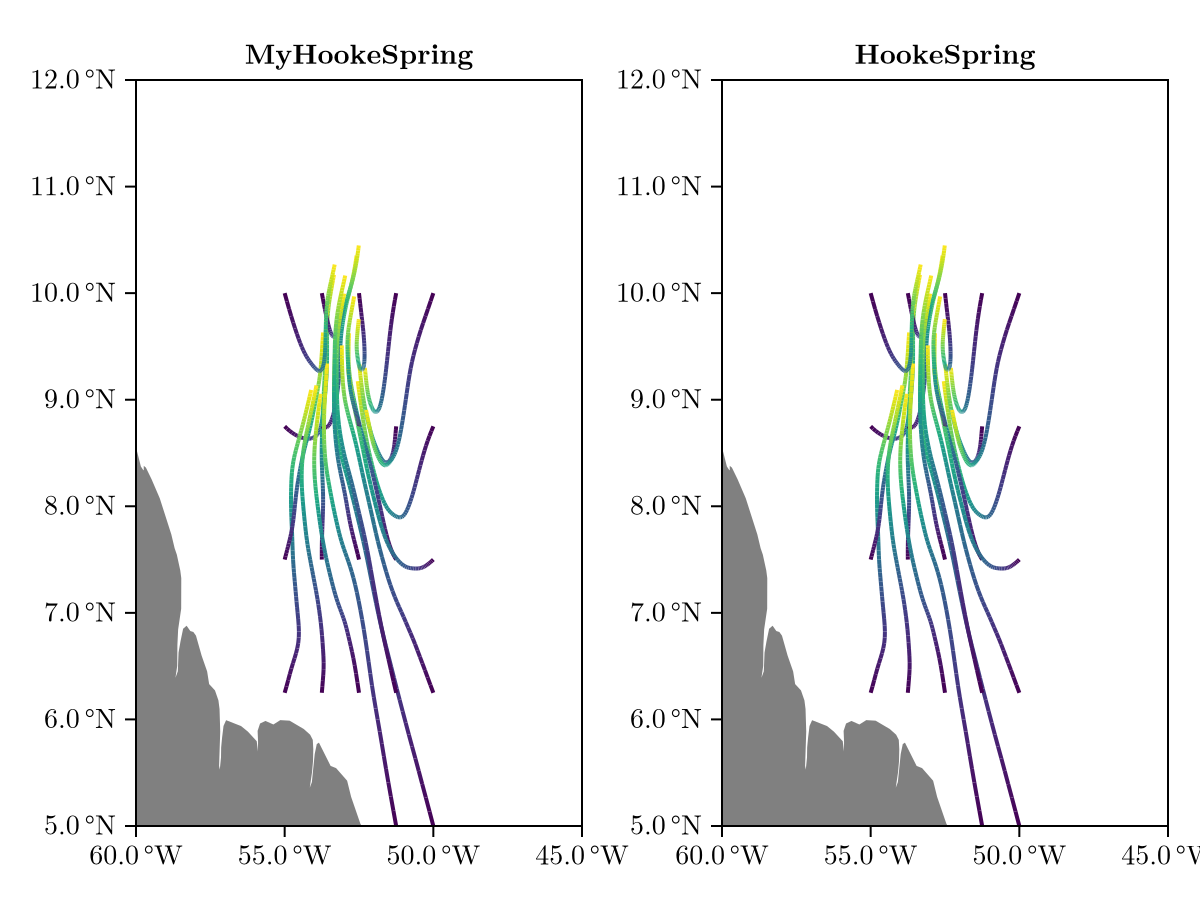
How to make HookeSpring

Next we'll make our own version of HookeSpring to see how to create a custom AbstractSpring. Much like the creation of an AbstractConnections, we create an object MyHookeSpring as a subtype <: of AbstractSpring that has two required fields. The first field is k, which should be function of one variable that represents the stiffness as a function of the separation between clumps. The second field is L, which should be a number equal to the natural length of the spring.

struct MyHookeSpring{F<:Function} <: AbstractSpring
    k::F
    L::Float64
end

From here you could define a custom constructor, or simply create instances of the spring manually. For example, for a spring of amplitude 1 and natural length 100 (in units of UNITS[distance]), we can simply do

my_spring = MyHookeSpring(x -> 1, 100.0)

Anonymous functions

Expressions such as x -> 1 are called anonymous functions. In brief, something like x -> x^2 + 1 is equivalent to defining a function that takes a single argument x and returns x^2 + 1. In the case of a Hooke spring, the stiffness is a constant, so the stiffness function maps the distance between two clumps to a constant value.

This is all that's required for an AbstractSpring. Let's see it an action vs. the stock HookeSpring.

tspan = (DateTime(2018, 4, 13), DateTime(2018, 4, 20)) .|> datetime2time
ics = InitialConditions(tspan, range(-55.0, -50.0, length = 5), range(5.0, 10.0, length = 5), to_xy = true)
n_clumps_max = size(ics.ics, 2)
clumps = ClumpParameters()
my_springs = MyHookeSpring(x -> 1, 100.0) # this is us!
springs = HookeSpring(1, 100.0) # the stock version, has a slightly different constructor (just rhs of x -> j)
connections = ConnectionsFull(n_clumps_max)
gd_model = ImmortalModel()
land = Land()

my_rp = RaftParameters(
    ics = ics,
    clumps = clumps,
    springs = my_springs,
    connections = connections,
    gd_model = gd_model,
    land = land,
    n_clumps_max = n_clumps_max
)

stock_rp = RaftParameters(
    ics = ics,
    clumps = clumps,
    springs = springs,
    connections = connections,
    gd_model = gd_model,
    land = land,
    n_clumps_max = n_clumps_max
)

my_rtr = simulate(my_rp)
stock_rtr = simulate(stock_rp)

fig = Figure()
ax = Axis(fig[1, 1], title = "MyHookeSpring", limits = (-60, -45, 5, 12))
viz!(ax, my_rtr)
land!(ax)

ax = Axis(fig[1, 2], title = "HookeSpring", limits = (-60, -45, 5, 12))
viz!(ax, stock_rtr)
land!(ax)

fig